#' The Probability Density for the Correlation Coefficient for
#' Uncorrelated Normal Distributions
#'
#' @param r The observed Pearson correlation
#' @param n The sample size
#'
#' @details
#' More details can be found here:
#' <https://en.wikipedia.org/wiki/Pearson_correlation_coefficient#Using_the_exact_distribution>
#'
#' A more complicated formula exists for the density of Pearson
#' correlation statistics calculated from bivariate normal
#' distributions with rho != 0.
#'
#' The reason for the inclusion of a normalizing constant was that I found that
#' integrating from -1 to 1 for positive integers n was not reflecting properly that
#' P(r in [-1,1]) = 1.
#'
cor_coef_density <- function(r, n) {
unnormalized_density <- function(r, n) {
(1/(1-r^2))^{-(n-1)/2} / (sqrt(n-2) * beta(1/2, (n-2)/2))
}
normalizing_constant_for_n <- integrate(f = unnormalized_density, lower = -1, upper = 1, n = n)[[1]]
return(unnormalized_density(r, n) / normalizing_constant_for_n)
}
# Probability of observing correlation coefficient of at least .25:
integrate(f = cor_coef_density, lower = 0.25, upper = 1, n = 100)
integrate(f = cor_coef_density, lower = 0.25, upper = 1, n = 20)
# In either sample sizes of 100 or 25, the probability of observing a
# Had to correct for the normalizing constant...
integrate(f = cor_coef_density, lower = -1, upper = 1, n = 20)
# Now check if it's right under a simulation study
n <- 24L
n_sims <- 100000L
observed_r <- numeric(length = n_sims)
for (i in 1:n_sims) {
X <- rnorm(n = n)
Y <- rnorm(n = n)
observed_r[i] <- cor(X,Y)
}
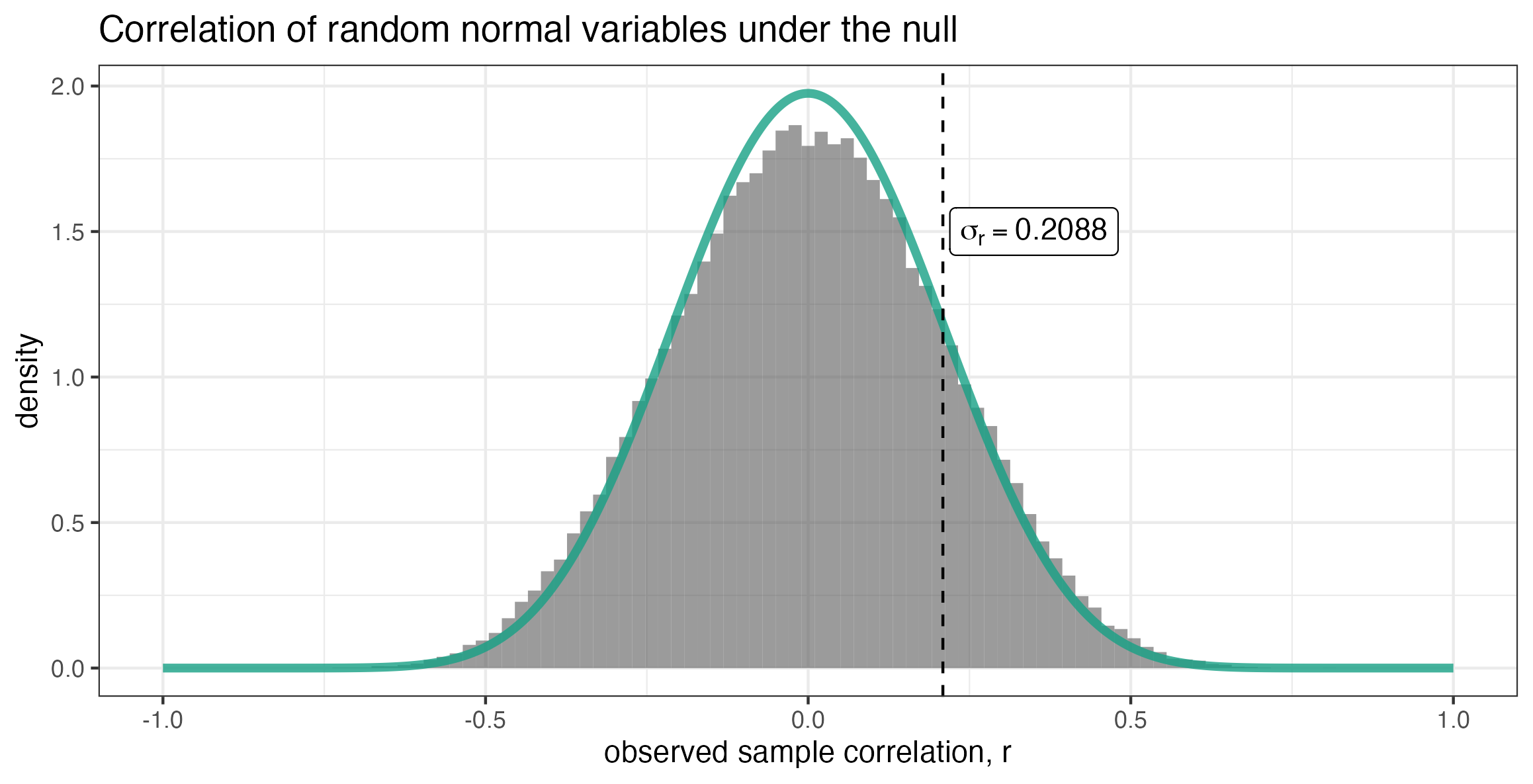
sd(observed_r)
library(ggplot2)
# looks like perhaps the approximation is slightly off? but it looks largely
# correct — and importantly, it seems to covary with the population size in the
# right way
ggplot() +
geom_histogram(
data = data.frame(observed_r = observed_r),
mapping = aes(x = observed_r, y = ..density..),
bins = 100, alpha = 0.6) +
geom_line(
tibble::tibble(
x = seq(-1,1,length.out=1000),
y = cor_coef_density(r = x, n = n)),
mapping = aes(x = x, y = y),
linetype = 'solid', color = '#16a085', linewidth=1.5, alpha = 0.8) +
geom_vline(
xintercept = 0.2088,
linetype = 'dashed') +
annotate(
geom = 'label',
label = expression(sigma[r] == "0.2088"),
x = .35,
y = 1.5) +
labs(x = "observed sample correlation, r", y = 'density') +
ggtitle("Correlation of random normal variables under the null") +
theme_bw() On Charles Spearman’s 1904 work, “‘General Intelligence,’ Objectively Determined and Measured”
Christian Testa and Anne Brandes
February 26, 2024
Introduction
- Who was Charles Spearman
- What were his motivations in writing?
- Main arguments
Who was Charles Spearman?
- Known for his work in psychology, Spearman was born in London in 1863 and died in 1945. His most famous work was on human intelligence
- He served in the army from 1883 to 1897, and then went to study at the University of Leipzig, where he was influenced by Wilhelm Wundt, the father of experimental psychology, or “new psychology”
- I.e., used empirical methods instead of metaphysical reasoning
- He was recalled to the army during the Second Boer War and served as a general
- Somehow, amidst all this, he published his most famous work in 1904

Image from Wikipedia: Charles Spearman
Who was Charles Spearman?
- Spearman was heavily persuaded by Galton’s work, particularly the creation of “Co-relation” from 1888.
- See, for example, Stigler’s 1989 article Francis Galton’s Account of the Invention of Correlation
- He was also influenced by the work of the French psychologist Alfred Binet, who was working on the first intelligence tests, e.g., “intelligence quotients”
- His seminal 1904 work posits that intelligence rests on a single, general (latent) factor, which he called “g”
- This was the first work in the field now called factor analysis
- He also developed rank correlation

Image from Wikipedia: Charles Spearman
What were his motivations in writing?
He sees psychology as an up-and-coming field, and yet also a subject looked down-upon by the scientific community.
He’s trying to make a case for psychology as a science, rooted in data analysis and empirical methods.

Page 202
What were his motivations in writing?
He is making clear he intends to lay down the scientific foundations of psychology, which will be (implicitly) comparable to Newton’s equations of motion —
Especially with an eye towards refuting the criticisms of psychology as puttering about.

Page 203
What were his main arguments?
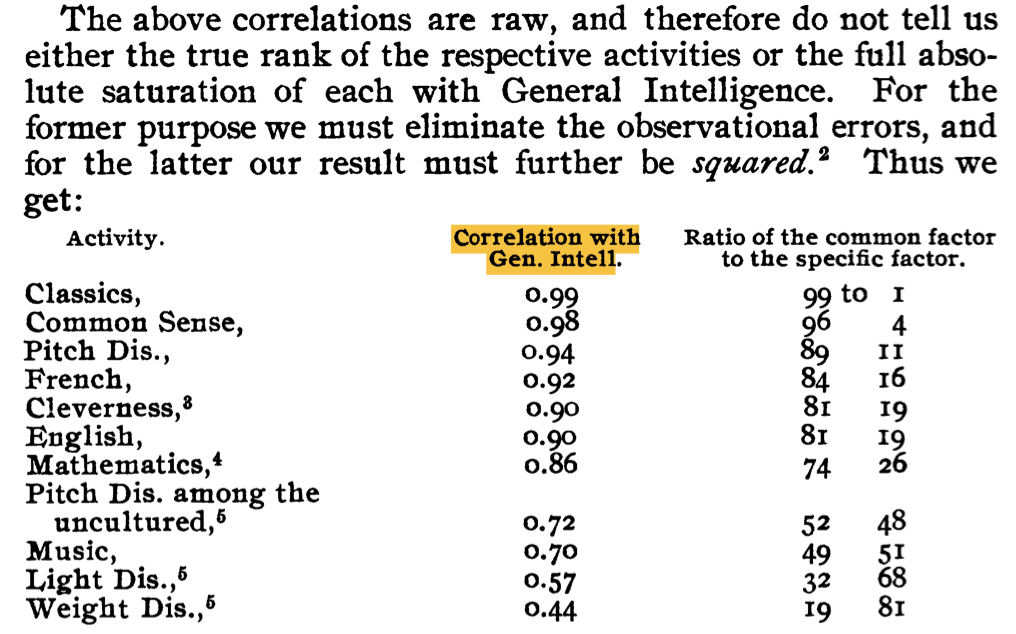
Spearman was analyzing data on children’s performance across various school tests, and he found that the scores were correlated.
In analyzing the data and their correlations, he hypothesized that there was a single, general factor that was responsible for the correlations and he called this the “g” factor.
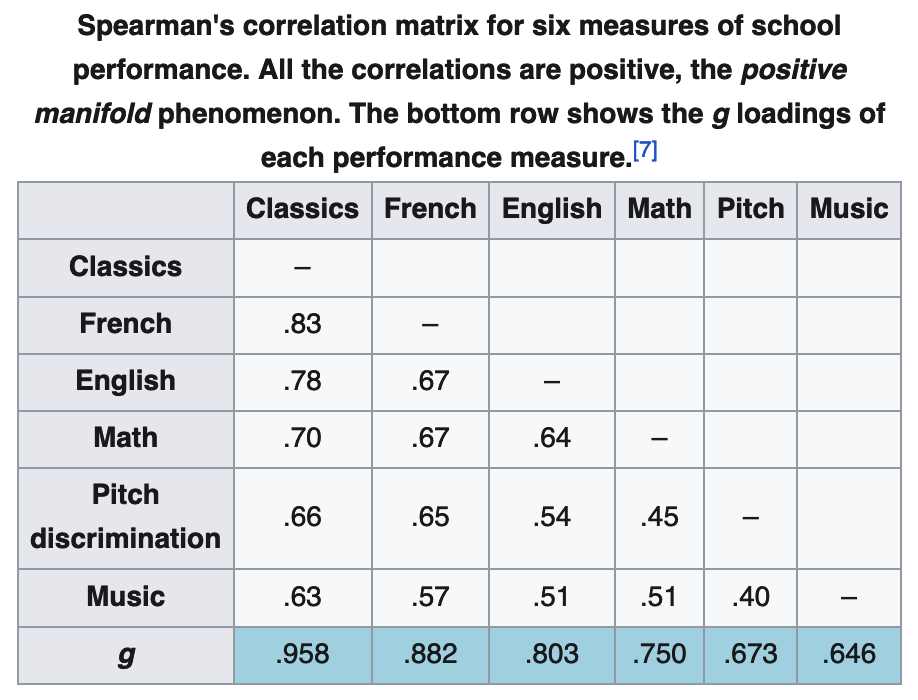
Table from Wikipedia : g factor
What were his main arguments?

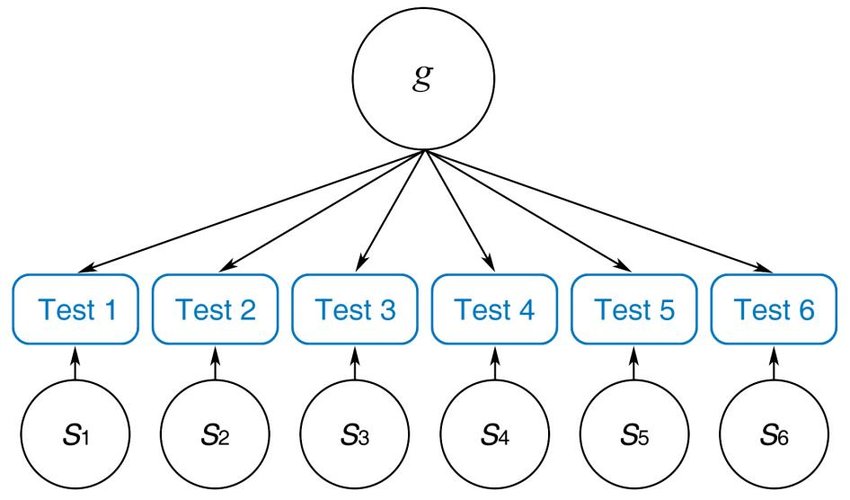

Page 205; Wikipedia : g factor
So let’s get into it
- What was the structure of his 1904 paper?
- What data did he use?
- What were the methodological innovations?
- How did he interpret his findings?
- What were the implications of his work?
Plan for the rest of the slides
- Go over the rest of the 1904 paper
- Have a section on contemporary uses of factor analysis
- Discuss the Bartholomew, Gould, Michell, and possibly Glymour papers
Structure of Spearman, 1904
After his introduction to the state of psychology and prior work, Spearman lays out his analysis plan for data collected on school children’s performance in “discrimination” and “intelligence” tests.
He covers some preliminarys on how to calculate correlation coefficients, including a method for “elimination of observational errors” and “elimination of irrelevant factors.” (It’s on Chapter II, pg 252 that he introduces rank correlation).
For a series of experiments, he presents the results of his correlational analyses with particular emphasis on 1) detrending for age, and 2) investigating which of the tests are correlated with each other.
Finally, he concludes with an analysis of the “General Intelligence” factor.
State of the art in 1904

Page 208
State of the art in 1904

Page 217
State of the art in 1904

Page 211
State of the art in 1904

Page 235
State of the art in 1904

Page 211
State of the art in 1904

Page 218
Data used
Spearman collected the following data:
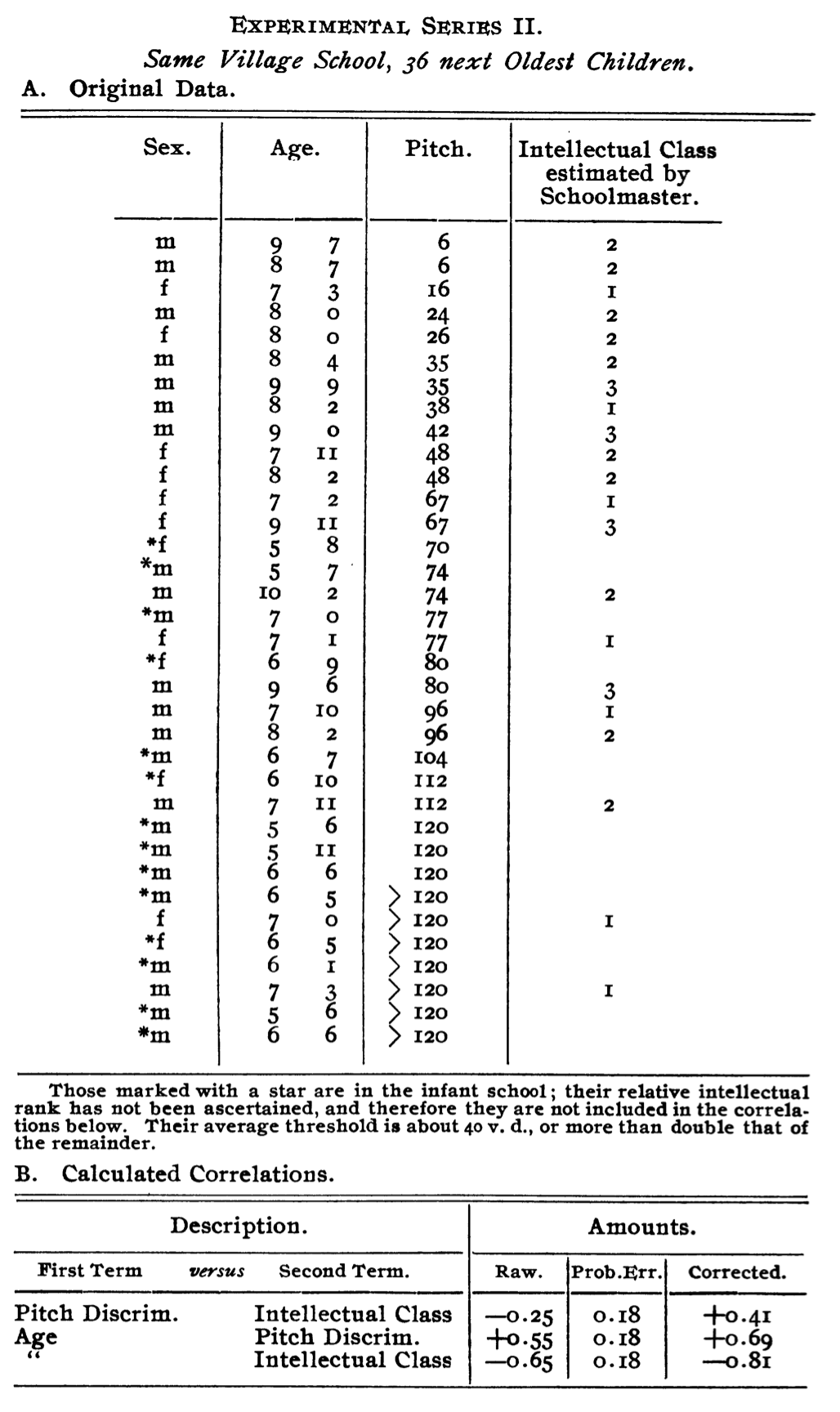
- Experiment I used the 24 oldest children tested in Light, Weight, and Sound
- Experiment II used the next 36 oldest children with tests only on Sound, interviewed collectively.
- Experiment III on Sight and Weight discrimination among boys from a preparatory school
- Experiment IV on Sound only in the high class preparatory school boys, with only particular intervals tested
- Experiment V, similar to experiment I with boys and girls, but aiming for higher variation rather than homogeneity
Intelligence Measures
- Examination scores and school rankings were thought to reveal “Present Capacity”
- School rankings divided by age were dubbed “Native Capacity”
- Teachers were asked to rank students based on their “general impression” (e.g., based on if they seemed “bright”, “average”, “dull”)
- Using a similar technique, the oldest of the children of Series I was asked to rank peer students based on their “common sense”, and then the next oldest child was asked to do the same.
Correlation
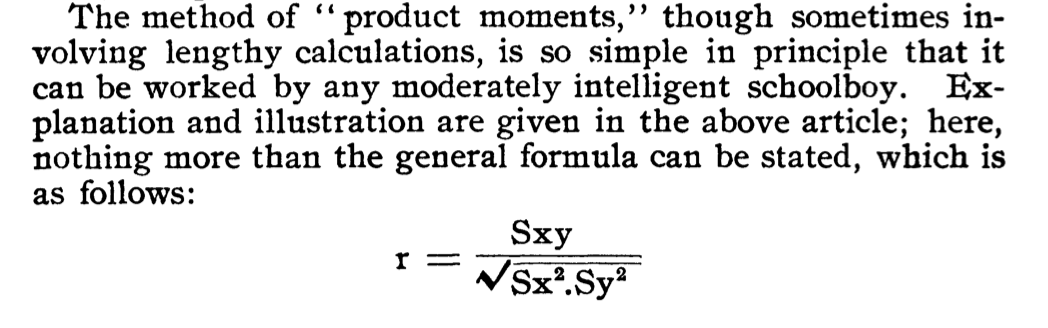

Page 252
Correlation — Elimination of Observational Errors

Page 253
Correlation — Elimination of Irrelevant Factors

Page 256
Results (intermangled with Interpretation)
Experiment I

Let’s Check His Math
What is the “probable error” of a correlation coefficient?
I’m not immediately sure about the distribution for Spearman’s rank correlation coefficient, but Pearson’s product-moment correlation has a known distribution.
The distribution for a sample correlation coefficient for correlated random normal variables is a little bit crazy…
\[ f(r) = \frac{(n-2) \Gamma(n-1)(1 - \rho^2)^{\frac{n-1}{2}} (1-r^2)^{\frac{n-4}{2}}}{ \sqrt{2\pi} \Gamma(n-\frac{1}{2})(1-\rho r)^{n - \frac{3}{2}} } {}_{2}{F}_1\left(\frac{1}{2}, \frac{1}{2}; \frac{1}{2}(2n-1); \frac{1}{2}(\rho r + 1)\right) \]
But for uncorrelated variables (the null hypothesis), the distribution is much simpler:
\[ f(r) = \frac{\left( \frac{1}{1-r^2}\right)^{-\frac{n-1}{2}}}{ \sqrt{n-2} B\left( \frac{1}{2}, \frac{n-2}{2} \right) }, \]
where \(B\) is the Beta function and \({}_2{F}_1\) is the Gaussian hypergeometric function.
Checking his math
Adjusting for “irrelevant factors”


Page 261-262
Conclusions from Experiment I

Page 263
Experiment II

Page 264
Experiment III

Page 265
Experiment IV

Page 265
Conclusions of Experiments

Page 268
Interpretation

Page 269
Conclusions of Experiments

Page 272
A “Theorem”

Page 273
Hierarchy of Factors

Page 274
Hierarchy of Factors

Page 275
Hierarchy of Factors
Page 276
His Discussion

Page 284
His Discussion

Page 284
Appendix
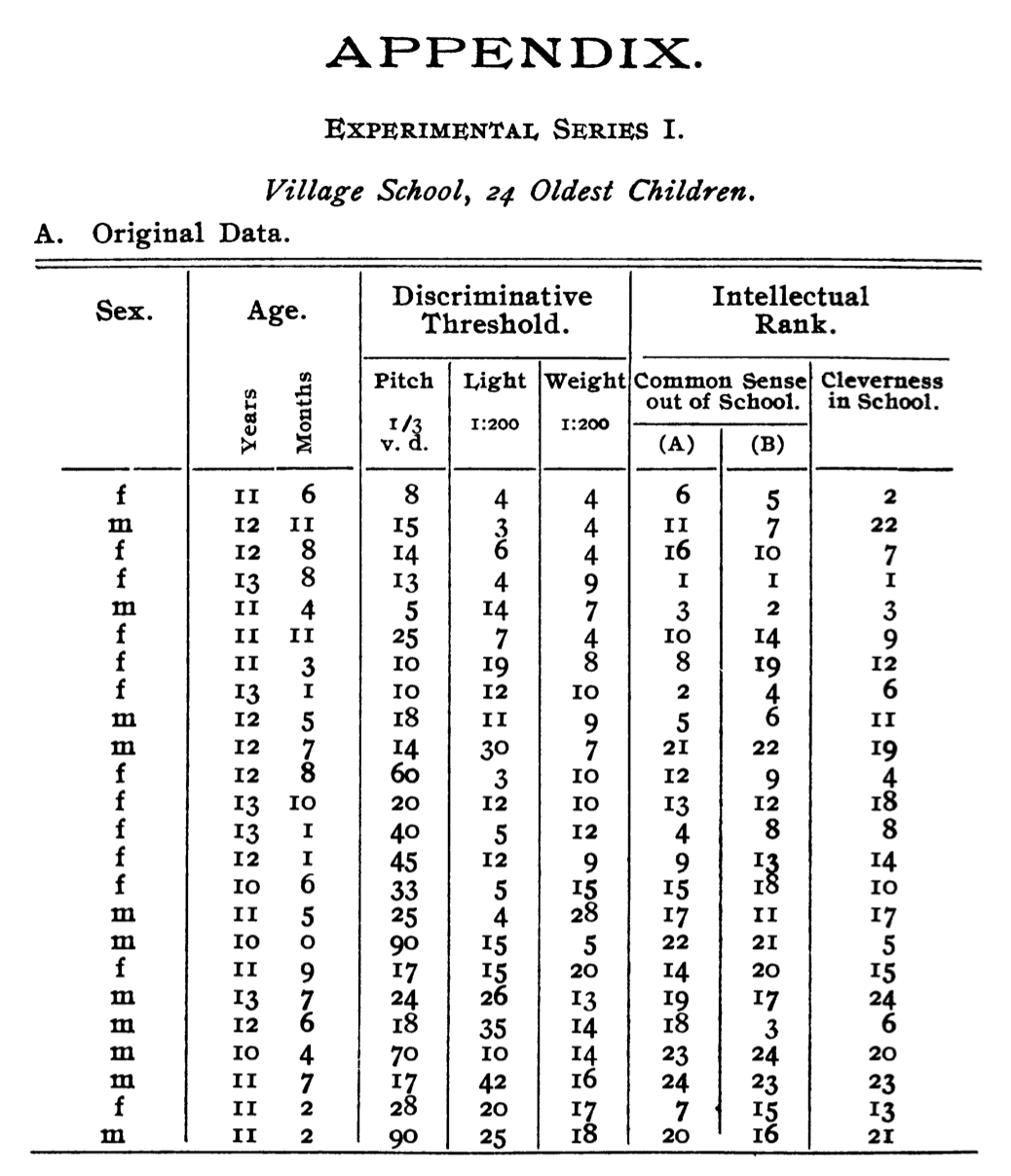
Page 286
Appendix
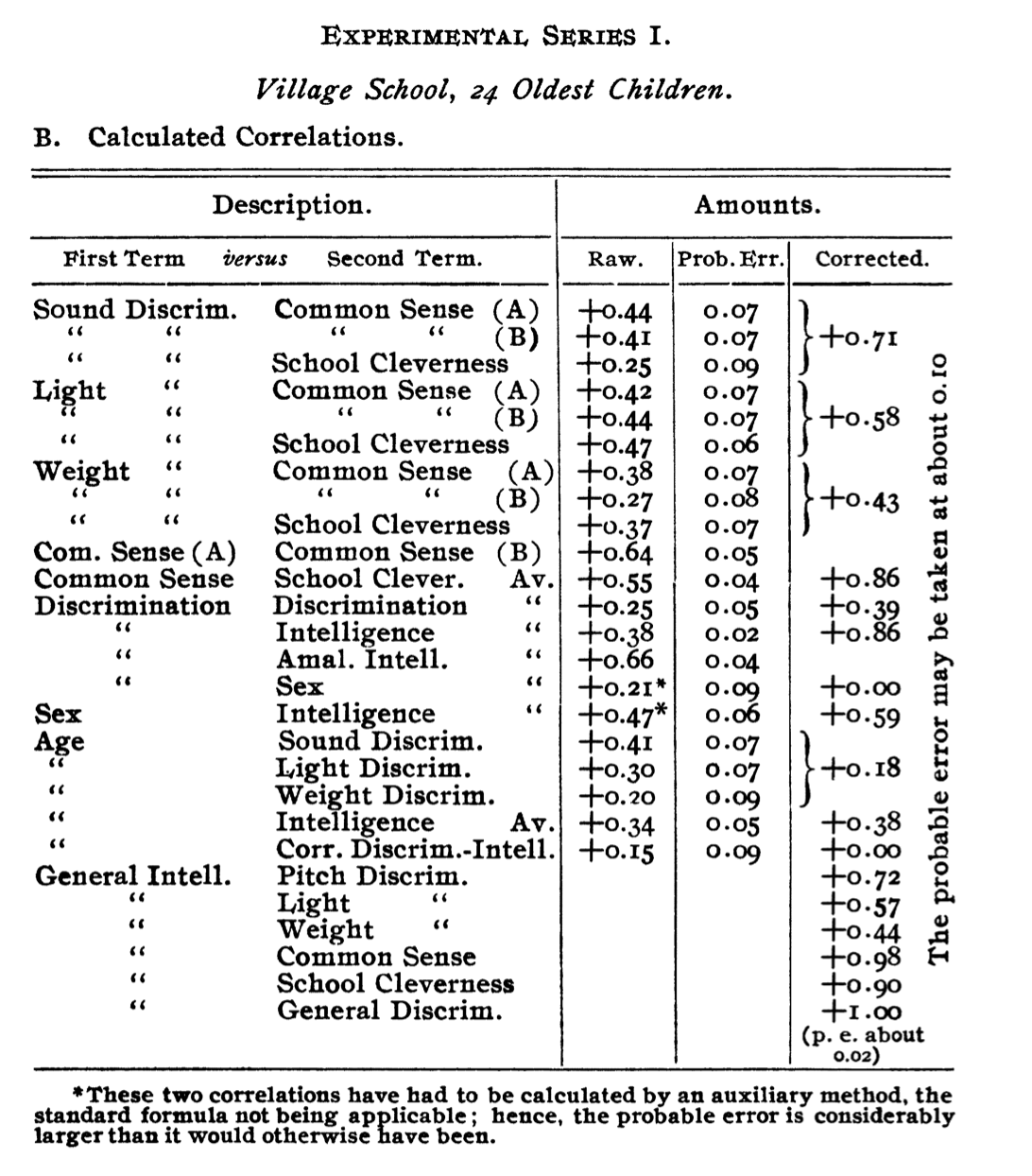
Page 287
Appendix
Page 288
Reflections
So what do we think?
Do we think he genuinely found evidence for a common factor shared by all forms/measures of intelligence?
And if not, where did his reasoning go wrong?
Reflections
- Merits:
- Asking teachers to rank their students on qualities like “common sense” and “general impression” was novel and what I would call an early ‘psychometric instrument’
- Such an instrument might have reasonable reliability, but its validity suffers from the fact that it’s based on potentially biased impressions of teachers.
- He was extraordinarily early in analyzing correlation matrices (though I’m not sure he formatted them like matrices) and recognizing their potential to have deeper structure.
- His work raises interesting questions about where “intelligence” ends and other skills begin.
- His literature review is fascinating.
Reflections
- Demerits:
- He offers no reflection how culture and (inherently subjective) definitions of intelligence interact.
- The text can be a bit clunky, and I think that’s because he didn’t have the language we have now like “Let \(X\) be a random variable.”
- While he does at times seem to be careful about calling for more investigation into what the General Intelligence factor is, he very quickly concludes that ‘General Intelligence’ “really exists.”
Contemporary Uses of Factor Analysis
Factor analysis has since been used in many fields, but especially psychology. It is common to see factor analysis in survey analysis (Qualtrics has a guide).
One workflow is to have respondents rate their agreement with a series of statements, then latent factors are identified from the responses using factor analysis, and factor scores describe how much variance of each observed variable is explained by each of the latent factors.
Spearman’s work only posited the existence of one common factor for intelligence measures, but after its development by Thurstone in the 1930-50s, factor analysis with multiple factors is now common.
Example
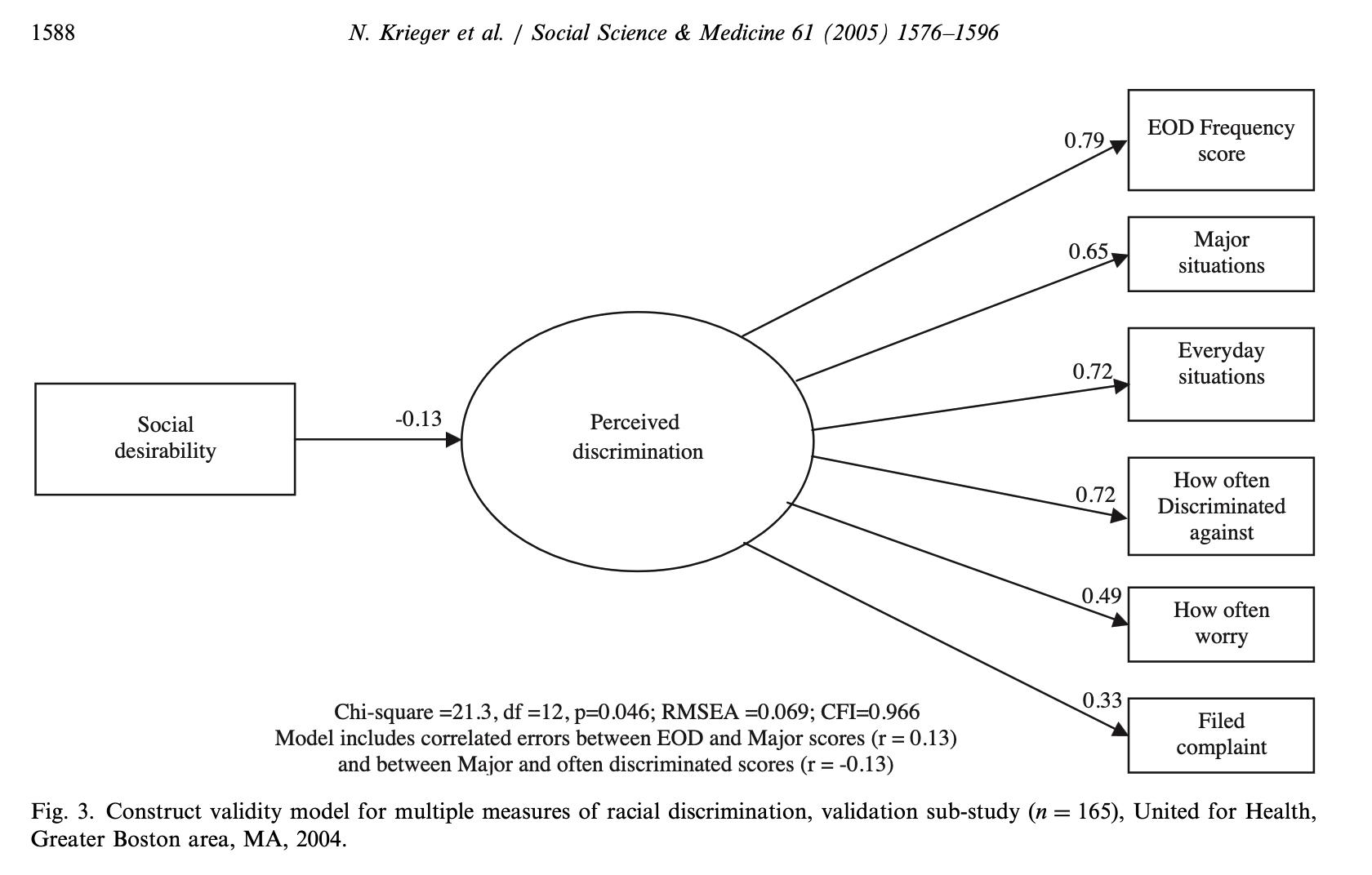
Krieger, N., Smith, K., Naishadham, D., Hartman, C., & Barbeau, E. M. (2005). Experiences of discrimination: validity and reliability of a self-report measure for population health research on racism and health. Social science & medicine (1982), 61(7), 1576–1596. https://doi.org/10.1016/j.socscimed.2005.03.006
Bartholomew, 2007
Bartholomew, D. J. (2007). Three faces of factor analysis. In R. Cudeck & R. C. MacCallum (Eds.), Factor analysis at 100: Historical developments and future directions (pp. 9–21). Lawrence Erlbaum Associates Publishers.

Gould, 1981
Gould, S. J. (1981). Mismeasure of Man. New York: Norton & Company
Chapter 6: The Real Error of Cyril Burt


Michell, 1997
Michell, J. (2023). “Professor Spearman has drawn over-hasty conclusions”: Unravelling psychometrics’ “Copernican Revolution”. Theory & Psychology, 33(5), 661–680. https://doi.org/10.1177/09593543231179446

Glymour, 1998
Glymour, Clark. “What Went Wrong? Reflections on Science by Observation and the Bell Curve.” Philosophy of Science, vol. 65, no. 1, 1998, pp. 1–32. JSTOR, http://www.jstor.org/stable/188173.

References
Direct References:
- Spearman, C. (1904). “General Intelligence,” Objectively Determined and Measured. The American Journal of Psychology, 15(2), 201–293. https://doi.org/10.2307/1412107
- Bartholomew, D. J. (2007). Three faces of factor analysis. In R. Cudeck & R. C. MacCallum (Eds.), Factor analysis at 100: Historical developments and future directions (pp. 9–21). Lawrence Erlbaum Associates Publishers.
- Gould, S. J. (1981). Mismeasure of Man, Chapter 6: The Real Error of Cyril Burt. New York: Norton & Company
- Michell, J. (2023). “Professor Spearman has drawn over-hasty conclusions”: Unravelling psychometrics’ “Copernican Revolution”. Theory & Psychology, 33(5), 661–680. https://doi.org/10.1177/09593543231179446
- Glymour, Clark. “What Went Wrong? Reflections on Science by Observation and the Bell Curve.” Philosophy of Science, vol. 65, no. 1, 1998, pp. 1–32. JSTOR, http://www.jstor.org/stable/188173.
Suggested References:
- William Revelle and the Personality Project (Writing Ongoing). “Ch. 6: Constructs, Components, and Factor models”, An introduction to psychometric theory with applications in R https://personality-project.org/r/book/
- Spearman (1904). “The proof and measurement of association between two things.” https://archive.org/details/proofmeasurement00speauoft/mode/2up
- “Factor analysis,” Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Factor_analysis&oldid=1197117979.
- Stephen M. Stigler. “Francis Galton’s Account of the Invention of Correlation.” Statist. Sci. 4 (2) 73 - 79, May, 1989. https://doi.org/10.1214/ss/1177012580
- Albano (2020). “Introduction to Educational and Psychological Measurement Using R, Chapter 8 Factor Analysis”. https://www.thetaminusb.com/intro-measurement-r/, published via bookdown.