Concepts of Algorithms
O Notation
- \(f(n) = O(g(n))\) means \(g(n)\) is an upper bound on \(f(n)\). As in, \(\exists c > 0, n_0 > 0\) such that \(0 \leq f(n) \leq cg(n)\) for all \(n \geq n_0\).
- \(f(n) = \Omega(g(n))\) means \(g(n)\) is a lower bound on \(f(n)\). As in, \(\exists c > 0, n_0 > 0\) such that \(0 \leq cg(n) \leq f(n)\) for all \(n \geq n_0\).
- \(f(n) = \Theta(g(n))\) means \(g(n)\) is a tight bound on \(f(n)\). As in, \(\exists c_1, c_2 > 0, n_0 > 0\) such that \(0 \leq c_1g(n) \leq f(n) \leq c_2g(n) \; \; \forall n \geq n_0\).
We can essentially think of these as \(O(g(n))\) being an upper bound, \(\Omega(g(n))\) being a lower bound, and \(\Theta(g(n))\) being a tight bound on the asymptotic runtime.
Asymptotic Complexity Classes
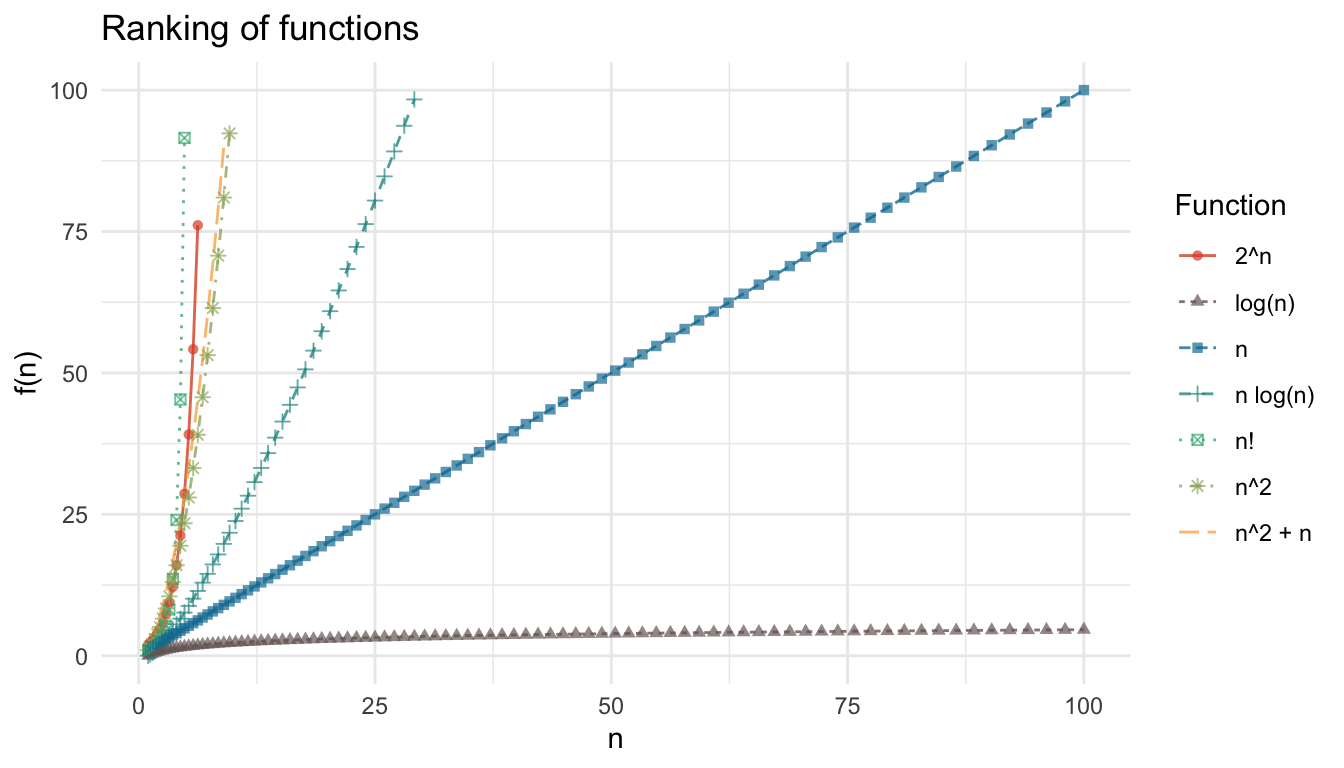
From the plot we can see that \(n!\) grows the fastest, followed by \(2^n\), \(n^2 + n\), \(n^2\), \(n \log n\), \(n\), and \(\log n\). In some kind of qualitative sense, we can see that \(n!\), \(2^n\), \(n^2 + n\), \(n^2\), and \(n \log n\) are all growing pretty rapidly in contrast to \(n\) which is about as good as any operation that reads data can get, and \(\log n\) which is the increasing slowest. This means we would much rather our algorithm’s time complexity be \(\log n\) or \(n\) compared to any of the others.
From the figure, we can see that \[O(\log n) \subseteq O(n) \subseteq O(n \log n) \subseteq O(n^2) = O(n^2 + n) \subseteq O(2^n) \subseteq O(n!).\]
More detail would be required to prove the result, but the above statement is nonetheless true. Recall that \(O(f) = \{ \text{functions }g \mid \exists \; c \in \mathbb{R}^+, n_0 \in \mathbb N^+ : 0 \leq g(n) \leq c f(n) \text{ for all } n \geq n_0 \}\).
Skiena (2020) writes this result as
Skiena, Steven S. 2020. The Algorithm Design Manual. 3rd ed. Texts in Computer Science. Springer. https://doi.org/10.1007/978-3-030-54256-6.
\[ n! \gg 2^n \gg n^3 \gg n^2 \gg n \log n \gg n \gg \log n \gg 1.\]
Rules for working with O-notation:
- \(O(f + g) = O(\max(f, g))\), same for \(\Omega\) and \(\Theta\).
- \(O(c \cdot f) = O(f)\) for constants \(c > 0\).
- \(O(f \cdot g) = O(f) \cdot O(g)\).
Links: